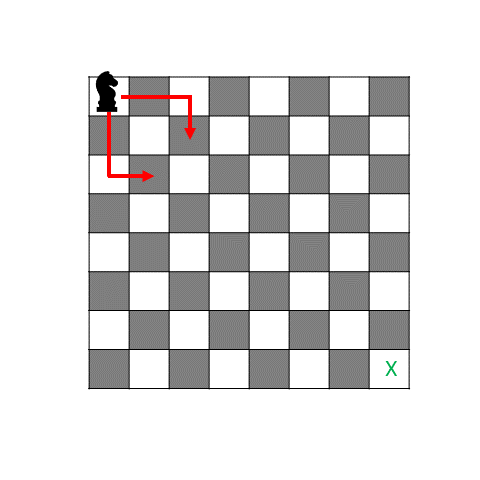
This puzzle is several hundred years old: on a standard chessboard, can a knight start in the top left corner, move to every square on the board exactly once, and finish in the bottom right corner? Why or why not? (The knight moves in an L, like the red arrows shown in the picture.)
There are a few ways to approach the problem. You might try it out, moving the knight around the chessboard as far as you can. But you’ll quickly see there are a lot of possibilities, and it’s going to be really hard to try them all!
One useful strategy when you’re faced with a problem that’s really big is to try a simpler version first. So start with a smaller board, say 3×3. You might see a problem really quickly. Now try 5×5. Explore for as long as you’d like – it’s still really hard to get the knight to go to every square, never mind ending up in the corner!
Hopefully you’ve had fun jumping the knight around, but you probably haven’t found any patterns. It just seems that there are more combinations than we can really study. Maybe we should think about this in a different way? Do you notice anything about the squares that the knight jumps to from one move to another? What about the squares the knight starts and ends on?
You may have noticed that a knight on a light square can only jump to dark squares, and a knight on a dark square can only jump to light ones. So as you hop your knight around, it goes 1. Light – 2. Dark – 3. Light – 4. Dark – 5. Light – etc. So odd steps are light, and even steps are dark. So if step 1 is on a light square (like the upper left corner), then all odd steps are light, and all even steps are dark. With an 8×8 chessboard there are 64 squares, which is an even number, so the last step has to be dark. But the bottom right square is light! So it can never end there. It can make a full tour though – in fact, there are 19,591,828,170,979,904 paths it can take if it starts and ends at any square!