The neighborhood kids are opening lemonade stands. What is the fewest number of houses that need lemonade stands in front so that no one has to walk more than one house away to get lemonade?
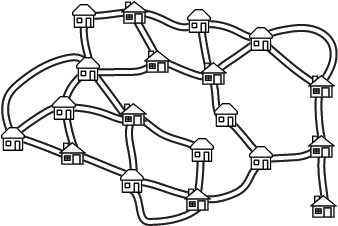
Scroll down for the solution:
What strategy did you use to solve this puzzle? The interesting thing about problems like these is that there is no one strategy that always works! First let’s try putting a lemonade stand at the house with the most connections. That way it can reach the most other kids, right?
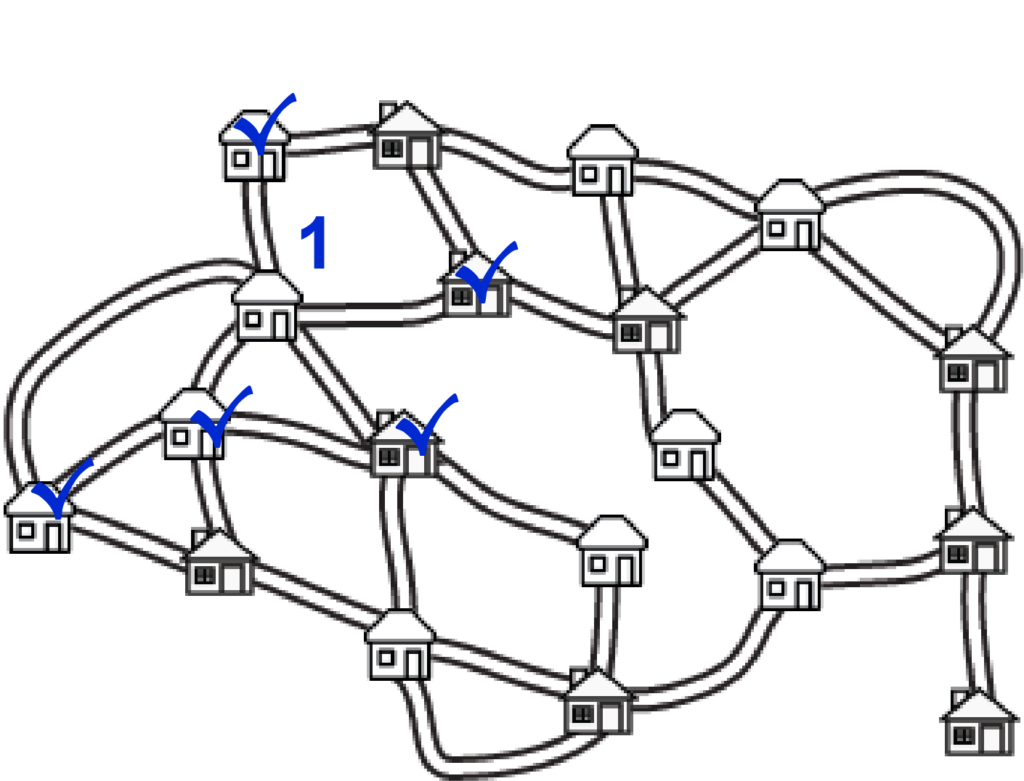
By putting a lemonade stand at 1, we reached five other houses. Great start! Let’s keep going with this strategy. There are no houses that reach four new houses, so we’ll put lemonade stands at site 2 and 3 where they’ll reach 3 more.
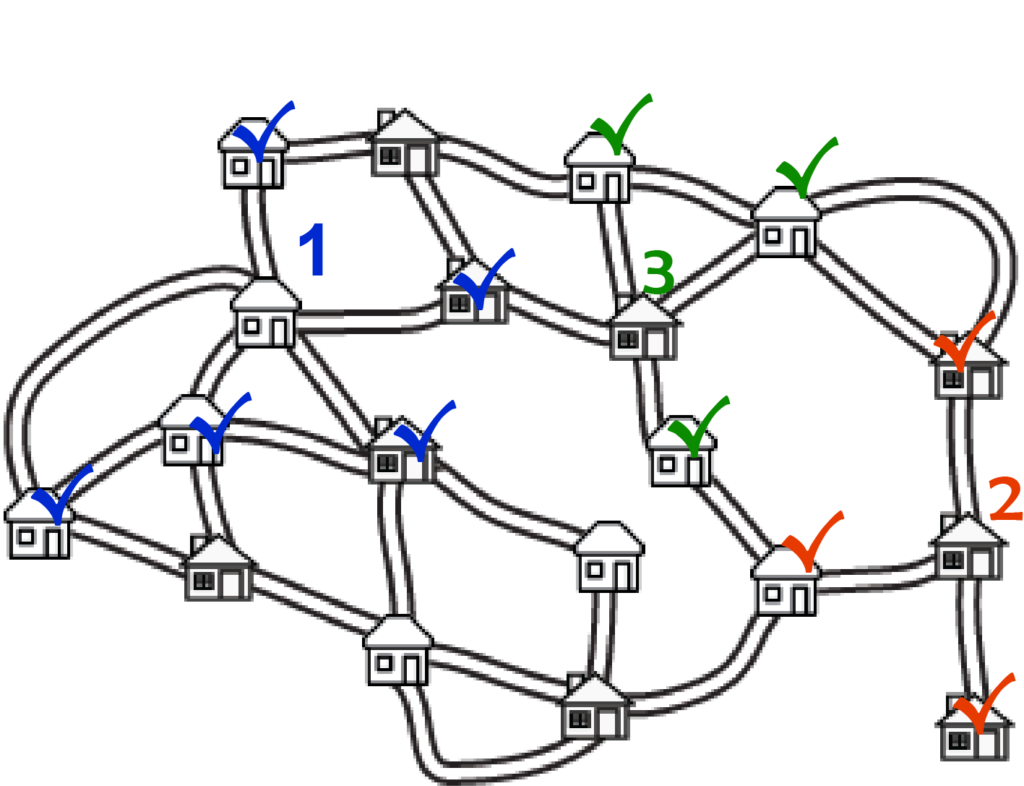
We just have a few houses left. Unfortunately, it’s going to take us two lemonade stands to cover the houses at the bottom of the map, and we still have a house up at the top that needs a stand. So we were able to do it with six stands. Not bad! But can we do better?
The strategy we used last time usually does pretty well, and sometimes the best. But with this map you might notice there is a house all by itself in the lower right-hand corner. If those kids are going to get lemonade, it has to come from their own house, or the one just up the street. Let’s start with one up the street, since it can get to more houses.
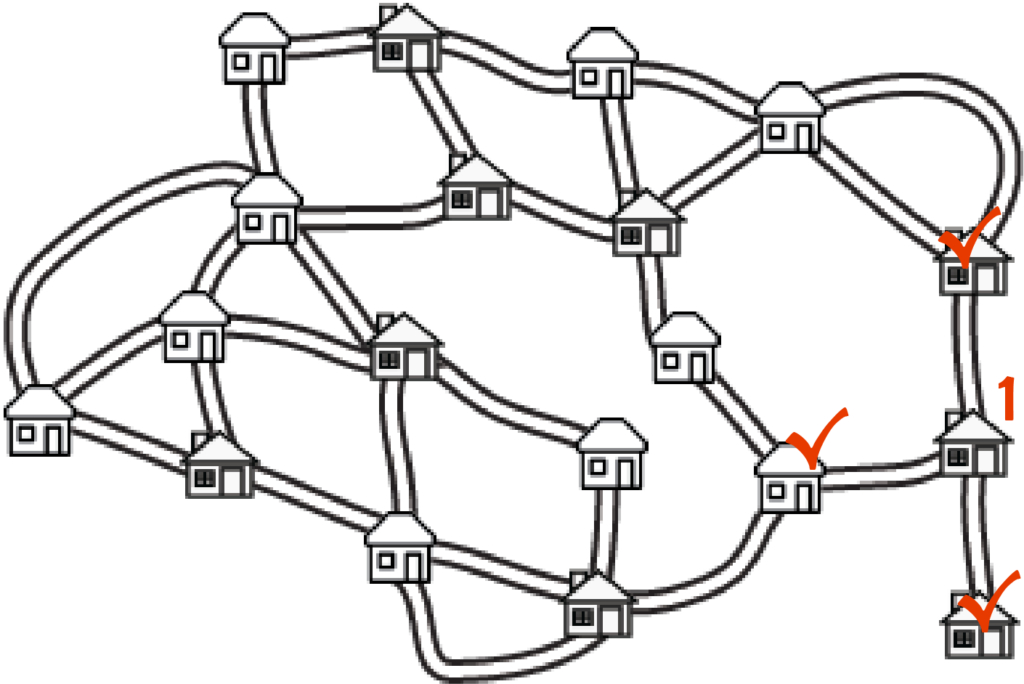
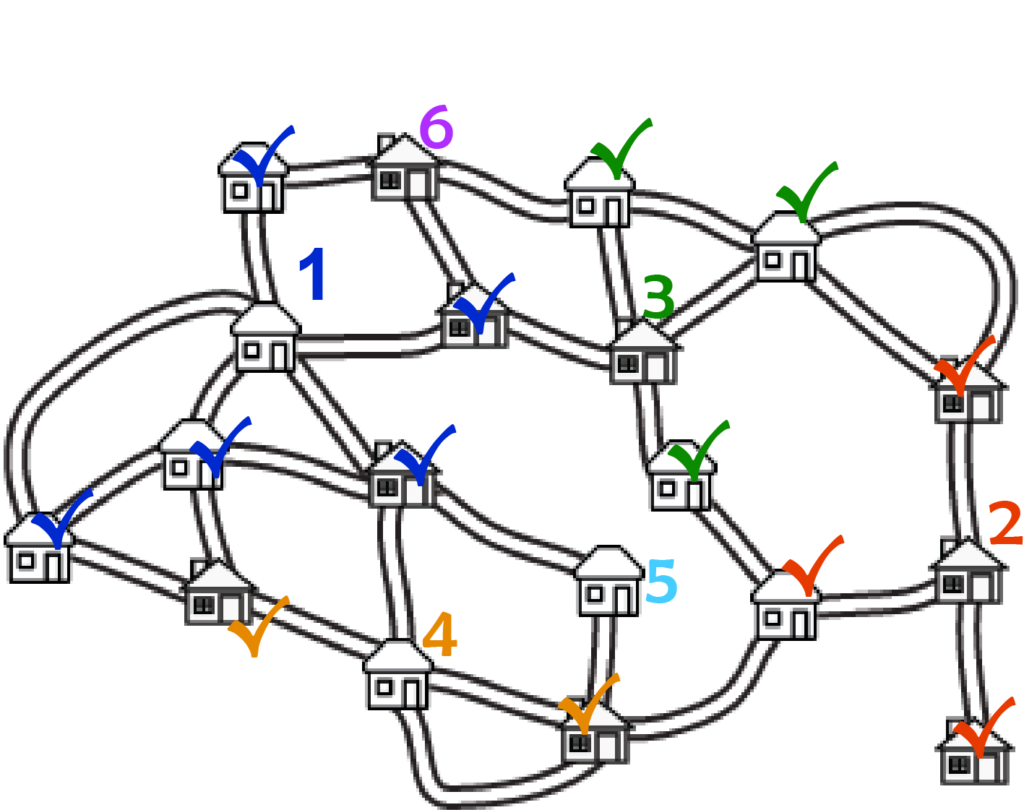
Now there’s another place where we know we need a stand – can you find it? Look for houses that can only get lemonade from other other place.
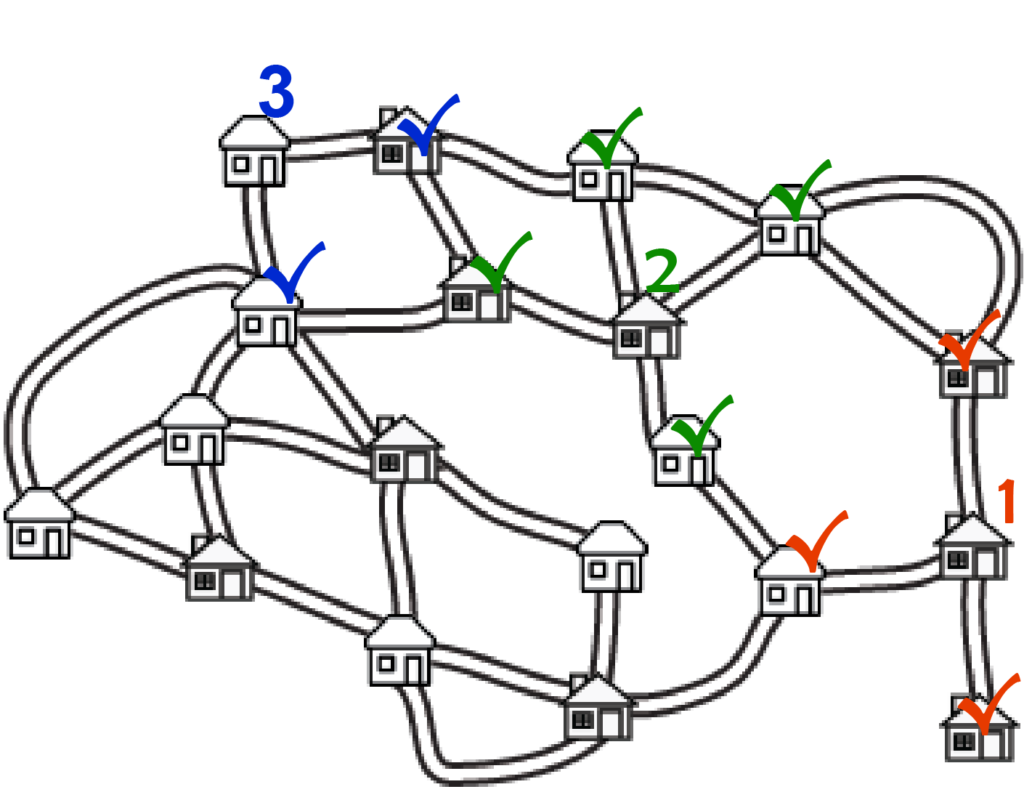
A lemonade stand at 2 gets the house below it (and three others). By the same idea, we can put a stand at 3. Notice the house we started with last time doesn’t have a lemonade stand this time, even though it has the most connections! We just have seven houses left to cover, and we can do that with just two lemonade stands. There are a couple of choices – here’s one:

This time we did it with just five stands! That’s the best you can do with this map. We can draw lots of other maps though. The cool thing about these types of problems is that they’re easier to draw up than to solve, and if you have a solution it’s easier to check if it’s right. To make your own, start by deciding where the lemonade stands will be. You can put them anywhere you want – it’s trickier if they’re in odd places.

The next step is to draw all the houses that will be connected to each lemonade stand. You can put them anywhere on the map you want, as long as they just have one connection to a lemonade stand. If you stopped now, the problem would be easy!
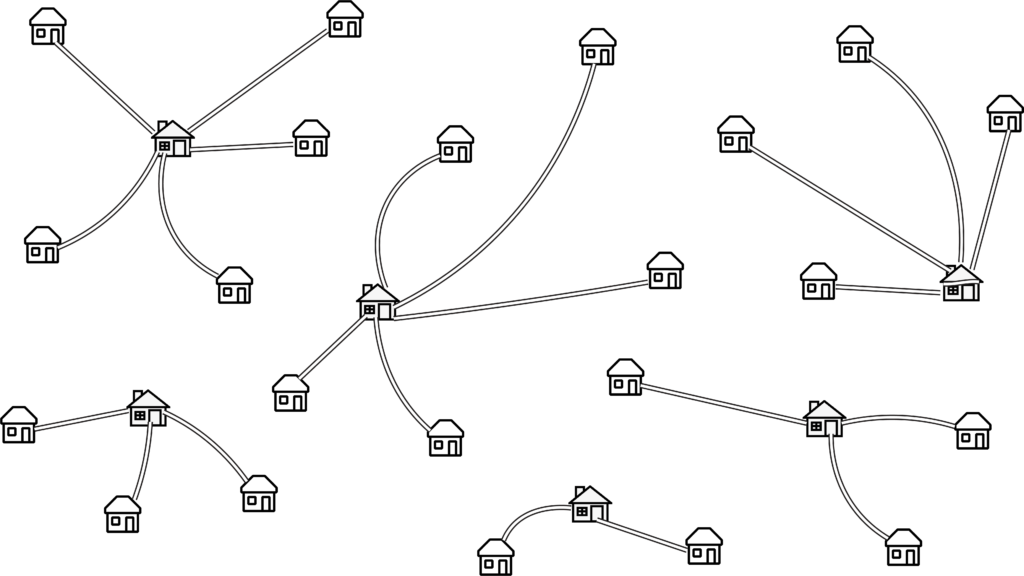
Now we want to add a lot more connections. Only connect houses that are served by different lemonade stands, and don’t connect directly to any lemonade stands. That way all these extra connections will hide where the lemonade stand needs to go, without changing the solution. The trickiest part here is keeping track of which houses are going to have lemonade stands! (In this map the houses look different – but that would give away the solution on your map.)

Now give your map to someone else, and see if they can solve it! You might notice that if you give them a small map, they can figure it out in a reasonable amount of time. They might come up with a good strategy, or they might just try every possibility. But if you give them a really big map, then it would take them forever to try everything, and they might never know if they have the right answer (until you tell them)!
To learn more: This is called an “NP problem”, which means that it takes a lot of time to solve it as the problem gets big, but it doesn’t take very long to check the solution once it’s been given to you. Sudoku is another example like this. Your passwords work and are kept secure because they’re based on an NP problem. Watch this great video to learn more about how all these problems are related.



