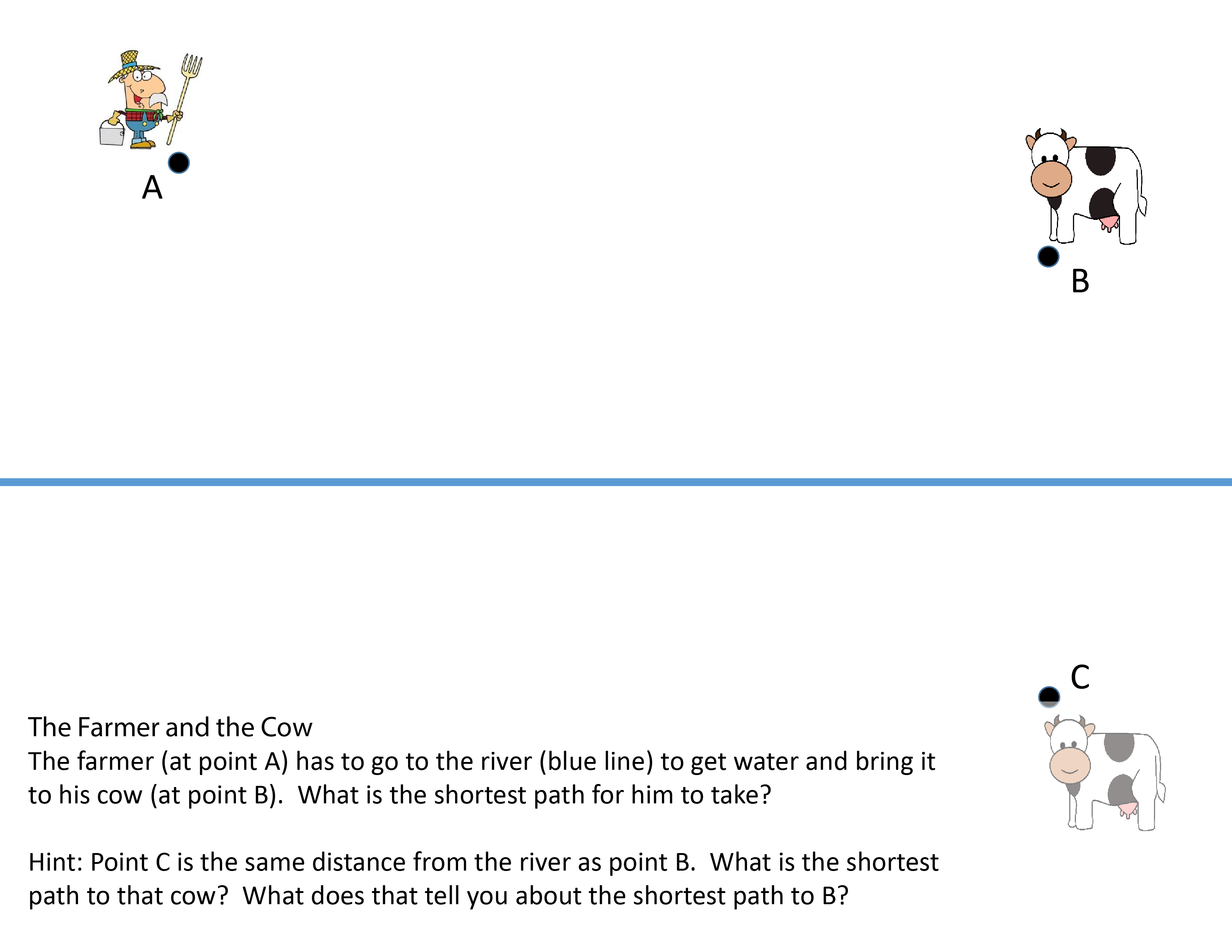
Scroll down for the answer:
There are a few ways to solve this problem. You could pick a point on that river, draw a line from the farmer to that point, and calculate the length of that line. You could then draw a line from that point to the cow, calculate its length, and add the two together. You could even solve for the minimum total length using calculus. But there’s a simpler way – start by imagining there’s another cow directly across the river from the real cow.
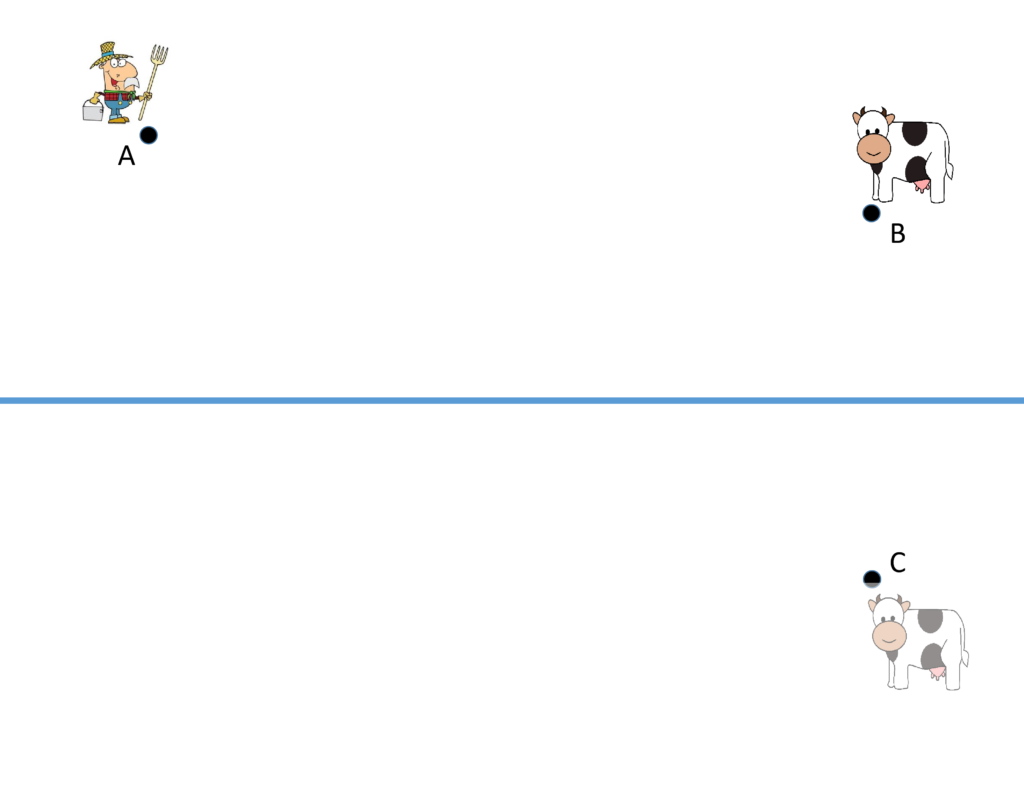
What’s the fastest way for the farmer to get from point A to the cow at point B? (Any path will cross the river, so we don’t have to worry about filling up the bucket!) You got it – a straight line! Below we’ve drawn the line to cow C, and put an X where it crosses the river.

The cool thing is that wherever X is, the distance from there to cow C is the same as the distance to cow B. That means that the total distance the farmer travels is the same whether he goes to cow B or cow C. So the shortest path must be the same – the one that goes to the river at X!
In this case we used a concept called “symmetry” to solve the problem much more easily than other strategies. Two objects are symmetric if you can match them by either turning, sliding, or flipping one of them. A good example of symmetry is when you look at yourself in the mirror – you see a “flipped” copy of yourself. In this case we flipped the cow across the river (just like if the river were a mirror). The flipped cow had a lot in common with the original – just like you look very similar to your image in the mirror.